Answer:
First, if we have a set of K elements, such that are ordered as:
{x₁, x₂, ...}
The total number of permutations for the K elements can be found in the next way.
For the first element in the set, we have K options.
For the second element in the set, we have (K - 1) options (because we already choose one)
For the third element we have (K - 2) options, and so on.
The total number of permutation is equal to the product between the numbers of options for each position's element, then the number of permutations for K elements is:
permutations = K*(K - 1)*(K - 2)*....*2*1 = K!
Now suppose that we have a set of N elements, and we want to make groups of K elements.
The total number of different combinations of K elements is given by the equation:
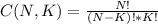
In this case we have 15 objects (then N = 15) and we take 7 at the time (Then K = 7)
Where we need to take in account the number of combinations and also the permutations for each combination.
Then the total number of different sets is:
C(15*7)*7!
First, the total number of combinations will be:
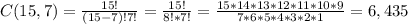
So we have 6,436 combinations, and each one of these combinations has 7! permutations.
permutations = 7! = 7*6*5*4*3*2*1 = 5,040
if we combine these we get:
Combinations*Permutations = 6,435*5,040 = 32,432,400