Question

What are the domain and range of f(x) = |x + 6|?

Answer 1

Domain:
`(-\infty, \infty)`

Range:
`f(x)\ge 0`

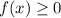
Explanation:

Interval Notation:

Interval Notation is one way to express a range of values. This is usually denoted with two values, let's just say "a" and "b" as:
`(a, b)` where "a" is less than "b", so the lower value goes on the left the higher values goes on the right.

The next thing to note is the difference between square brackets and parenthesis. Whenever you use a square bracket next to a value in interval notation, that means the value is included. If you use a parenthesis, that means the value is not included.

So for example:
`(2, 4]` means all values between 2 (excluding 2) and 4 (including 4)

Domain of a Function:

The domain of a function, or a relation, can be defined as all x-values that are on the graph. In most cases this is all real numbers which can also be denoted as:
`(-\infty, \infty)` which is saying all values between negative infinity and positive infinity.. which is any real number. The only time the domain doesn't include x-values, is because the line isn't defined at that x-value OR based on the context, only certain values are in the domain e.g (time after an event; only positive numbers)

In the function provided:
`f(x)=|x+6|` there is no x-value in which this function is undefined. So the range is all real numbers or
`(-\infty, \infty)`

Range of a Function:

The range of a function, or a relation, similar to the domain, can be defined as all y-values that are on the graph.

Now to determine the range of the function, we first need to understand what the absolute value is doing to the (x+6) inside of it.

The absolute value of any real number can be defined as the distance from zero. When applied to any positive number, the value stays the same (since thd distance from zero IS that number). When applied to any negative number, the value becomes the positive value of that number since distance is positive. For example -6 has a distance of 6 units to the left of zero, but distance is a scalar it doesn't care about the direction, it's just 6 units away from zero, which is why it becomes positive when taking the absolute value. When applied to zero... it just stays zero, since 0 is 0 units away from zero...

So the minimum value of |x+6| is going to be zero, which occurs when x+6 is equal to zero. If it's a negative number or positive number inside it's always going ot output a positive number. And for positive numbers it actually remains positive, so once it reaches the turning point (where it goes from increasing to decreasing) it's going to keep increasing to positive infinity.

This means the range is all values greater than or equal to zero, which can be denoted as:
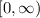`[0, \infty)` OR
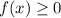`f(x)\ge 0` since the f(x) represents the "y" value, all the inequality is saying, is that the y-value will always be greater than or equal to zero.