Question

Find two consecutive odd integers whose squares add up to 290.

Answer 1

11, 13

Explanation:

Let one of the odd positive integer be x , then the other odd positive integer is x+2.

Their sum of squares:

`x^(2) +(x+2)^(2)`

`x^(2) +(x+2)(x+2)`

`x^(2) +x^(2) +4x+4`

`2x^(2) +4x+4`

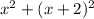
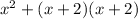
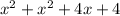
Given that their sum of squares = 290

`2x^(2) +4x+4 =290`

`2x^(2) +4x = 286`

`2x^(2) +4x -286 = 0`

`x^(2) +2x -143 =0`

`x^(2)+13x-11x-143 =0`

`x(x+13)-11(x+13)=0`

`(x+13)(x-11)=0`

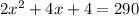
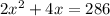
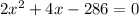
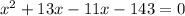
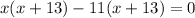
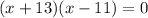
Therefore x = 11, x=-13

We take positive value of x:

So, x =11 and (x+2)= 11+2=13

Therefore , the odd positive integers are 11 and 13