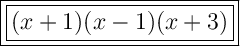Answer:
B. (x + 1)(x - 1)(x + 3)
Explanation:
To factor the polynomial x³ + 3x² - x - 3, we can start by grouping terms and then using the factoring by grouping method.
Group the first two terms and the last two terms:
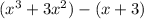
Factor out the greatest common factor from each group:
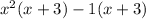
As both groups have a common factor of (x + 3), we can factor out the common factor:
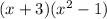
Notice that (x² - 1) is the difference of two squares (x² - 1²).
Therefore, factor (x² - 1) using the difference of two squares formula, a² - b² = (a + b)(a - b):
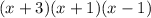
Rearrange the factors to match the order given in the answer options:

So, the factored form of the polynomial x³ + 3x² - x - 3 is: