Question

In the diagram below, assume that all points are given in rectangular coordinates. Determine the polar coordinates for each point using values of rr such that r≥0 and values of θ such that 0≤θ<2π. Visually check your answers to ensure they make sense.

(x,y)=(2,5) corresponds to (r,θ)=

(x,y)=(−3,3) corresponds to (r,θ)=

(x,y)=(−5,−3.5) corresponds to (r,θ)=

(x,y)=(0,−5.4)corresponds to (r,θ)=
​

Answer 1

Explanation:

We have cartisean points. We are trying to find polar points.

We can find r by applying the pythagorean theorem to the x value and y values.

`r {}^(2) = {x}^(2) + {y}^(2)`

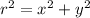
And to find theta, notice how a right triangle is created if we draw the base(the x value) and the height(y value). We also just found our r( hypotenuse) so ignore that. We know the opposite side and the adjacent side originally. so we can use the tangent function.

`\tan(x) = (y)/(x)`

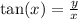
Remeber since we are trying to find the angle measure, use inverse tan function

`\tan {}^( - 1) ( (y)/(x) ) =`

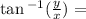
Answers For 2,5

`{2}^(2) + {5}^(2) = √(29) = 5.4`

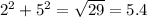
So r=sqr root of 29

`\tan {}^( - 1) ( (5)/(2) ) = 68`

So the answer is (sqr root of 29,68).

For -3,3

`{ -3 }^(2) + {3}^(2) = √(18) = 3 √(2)`

`\tan {}^( - 1) ( (3)/( - 3) ) = - 45`

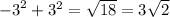
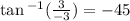
Use the identity

`\tan(x) = \tan(x + \pi)`

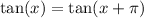
So that means

`\tan(x) = 135`

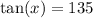
So our points are

(3 times sqr root of 2, 135)

For 5,-3.5

`{5}^(2) + {3.5}^(2) = √(37.25)`

`\tan {}^( - 1) ( ( - 3.5)/( - 5) ) = 35`

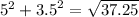
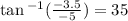
So our points are (sqr root of 37.25, 35)

For (0,-5.4)

`{0}^(2) + { - 5.4}^(2) = \sqrt{} 29.16 = 5.4`

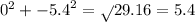
So r=5.4

So our points are (5.4, undefined)