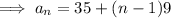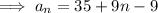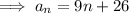Question

Write an explicit formula for
35, 44, 53, ....
an,the nth term of the sequence

Answer 1

`a_n=9n+26`

Explanation:

An explicit formula for a sequence allows you to find the nth term of the sequence.

To determine if the sequence is arithmetic or geometric, calculate the differences between the terms:

`35 \underset{+9}{\longrightarrow} 44 \underset{+9}{\longrightarrow} 53`

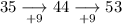
As the first differences are the same, the sequence is arithmetic with a common difference, d, of 9.

`\boxed{\begin{minipage}{8 cm}\underline{General form of an arithmetic sequence}\\\\$a_n=a+(n-1)d$\\\\where:\\\phantom{ww}$\bullet$ $a_n$ is the nth term. \\ \phantom{ww}$\bullet$ $a$ is the first term.\\\phantom{ww}$\bullet$ $d$ is the common difference between terms.\\\phantom{ww}$\bullet$ $n$ is the position of the term.\\\end{minipage}}`

Substitute a = 35 and d = 9 into the formula to create an explicit formula for the nth term of the sequence:

`\implies a_n=35+(n-1)9`

`\implies a_n=35+9n-9`

`\implies a_n=9n+26`