Answer:

Explanation:
Given:
Radius [r] = 3
Height [h] =7
To Find:
Volume of the cone
Solution:
We need to use the formula of volume of cone to find the volume of cone.
So We know that,
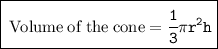
Where,
- π = 22/7[According to the question]
- r = radius
- h = height
So put their values in the formulae:
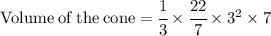
Now Simplify to find the value of cone.
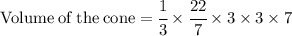
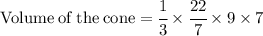
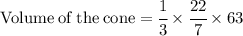
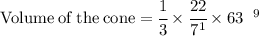
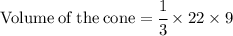
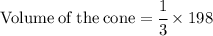
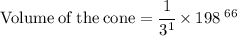
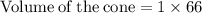

Hence, the volume of the cone would be 66 units^3 .

I hope this helps!