Question

A cylindrical diving bell is open at the bottom and closed at the top, and is 5m tall. The bell is open to atmospheric air until it is placed in the water, but the bell remains upright (open end facing down, closed end facing up). The pressure of the air inside the bell will naturally increase by 105 Pa for every 10m of depth the bell descends within the water. Assume the temperature of the air remains constant for this process, and that the air can be approximated as an ideal gas

Required:
a. If the bell is lowered 40 meters below the surface, how many meters of air space are left inside the bell?
b. Explain why water doesn't completely flood the bell as it enters the water V (m).

Answer 1

a) y = 0.35 m, b) hydrostatic balance

Step-by-step explanation:

a) For this fluid mechanics exercise, let's use that the pressure at a given level is the same, let's set a level on the bell shape.

The pressure inside is

P_interior = P₀ + ρ g h ’

The pressure outside

P_exterior = Pₐ + ρ g h

as the point is at the same level the pressures are equal

P_interior = P_exterior

P₀ + ρ g h ’= Pₐ + ρ g h

h ’= (Pₐ- P₀) + ρ g h

To calculate P₀ they indicate that the pressure increases 10⁵ Pa for every 10 m, we use a direct rule of proportions or rule of three

P₀ = 10⁵ (40 + h ’) / 10 = 4 10⁵ + h’ 10⁴

the positive sign is because the water inside the hood also increases the air pressure.

we substitute

(4 10⁵ + h’ 10⁴) + ρ g h’ = Pₐ + ρ g h

h’ (ρ g + 10⁴) = Pₐ - 4 10⁵ + ρ h h

h’ (1000 9.8 + 10⁴) = (1 10⁵ -4 10⁵) + 1000 9.8 40

h' (1.98 10⁴) = -3 105 + 3.92 10⁵

h’ =
`- (0.92 \ 10^5 )/(1.98 \ 10^4 )`

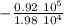
h ’= -4.65 m

as the hood is only 5 m high, the free air space is

Y = 5 - 4.65

y = 0.35 m

it is very little free space

B) The pressure outside and inside the hood is the same, the water rises inside the hood until the pressures equalize and at this point the force is equal and in the opposite direction, which is why the system is in hydrostatic balance.