Answer:
1. x = -9
2. a = 14
3. n =
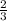
Explanation:
Here are the steps to the first question:
1. Rearrange Terms
61 = 7 - 6x
61 = -6x + 7
2. Subtract 7 from both sides
61 = -6x + 7
61 - 7 = -6x + 7 - 7
3. Simplify
Subtract the numbers:
61 - 7 = -6x + 7 - 7
54 = -6x + 7 - 7
Subtract the numbers:
54 = -6x + 7 - 7
54 = -6x
4. Divide both sides by the same factor
54 = -6x
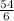 =
=
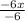
5. Simplify
Divide the numbers:
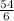 =
=
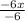
-9 =
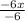
Cancel terms that are in both the numerator and denominator:
-9 =
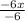
-9 = x
Move the variable to the left:
-9 = x
x = -9
Solution to Question 1:
x = -9
Here are the steps to the second question:
1. Combine multiplied terms into a single fraction
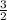 a - 26 = -5
a - 26 = -5
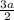 - 26 = -5
- 26 = -5
2. Find common denominator
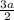 - 26 = -5
- 26 = -5
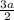 +
+
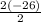 = -5
= -5
3. Combine fractions with common denominator
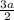 +
+
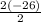 = -5
= -5
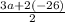 = -5
= -5
4. Multiply the numbers
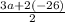 = -5
= -5
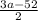 = -5
= -5
5. Multiply all terms by the same value to eliminate fraction denominators
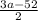 = -5
= -5
2 ·
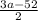 = 2(-5)
= 2(-5)
6. Cancel multiplied terms that are in the denominator
2 ·
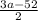 = 2(-5)
= 2(-5)
3a - 52 = 2(-5)
7. Multiply the numbers
3a - 52 = 2(-5)
3a - 52 = -10
8. Add 52 to both sides
3a - 52 = -10
3a - 52 + 52 = -10 + 52
9. Simplify
Add the numbers:
3a - 52 + 52 = -10 + 52
3a = -10 + 52
Add the numbers:
3a = -10 + 52
3a = 42
10. Divide both sides by the same factor
3a = 42
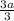 =
=
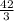
11. Simplify
Cancel terms that are in both the numerator and denominator:
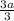 =
=
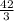
a =
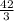
Divide the numbers:
a =
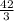
a = 14
Solution to Question 2:
a = 14
Here are the steps to the third question:
1. Divide the numbers
4 = n +
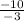
4 = n +
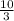
2. Subtract
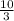 from both sides
from both sides
4 = n +
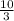
4 -
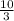 = n +
= n +
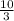 -
-
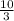
3. Simplify
Subtract the numbers:
4 -
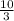 = n +
= n +
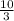 -
-
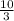
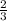 = n +
= n +
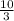 -
-
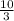
Subtract the numbers:
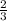 = n
= n
Move the variable to the left:
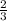 = n
= n
n =
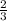
Solution to Question 3:
n =
I hope my answer helped you! If you need more information or help, comment down below and I will be sure to respond if I am online. Have a wonderful rest of your day!