Does 3+4x is less than or equal to 2(1+2x have a solution

Question

asked Oct 9, 2023 54.6k views

2 Answers

Ashtonium · Answer 1 · 2023-10-11T22:53:34+0000

Answer:

NO

Explanation:

You need x on one side of the equation.

3+4x ≤ 2(1+2x)

3+4x ≤ 2+4x

-4x -4x

3 ≤ 2

Since there is no x value there is no solution

Aniruddh Parihar · Answer 2 · 2023-10-15T15:14:15+0000

Answer:

No solution

Explanation:

Given inequality:

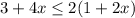
$3+4x \leq 2(1+2x)$

To determine if the given inequality has a solution, we can solve it step by step.

Begin by expanding the brackets on the right side of the inequality:

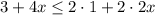
$3+4x\leq 2\cdot 1+2\cdot 2x$

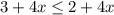
$3+4x \leq 2+4x$

Now, subtract 4x from both sides to isolate the constant terms:

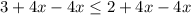
$3+4x-4x \leq 2+4x-4x$

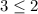
$3 \leq 2$

As 3 is not less than or equal to 2, there is no solution to the inequality since the inequality has led to a contradiction.

Therefore, the two sides of the inequality will never be equal or allow for 3 + 4x to be less than 2(1 + 2x) for any value of x.