Question

A circle with center C has equation x²+y²- 2x + 10y-19 = 0

It can be shown that center C is (1,-5) and that the radius is √45.
Find the equation of the tangent to the circle at the point (7,-2), giving your answer in the form ax + by + c=0, where a, b and c are integers.

Answer 1

2x + y - 12 = 0

Explanation:

The Tangent line will Always be perpendicular to the radius of a circle.

1. Find the slope of the radius that goes from the Center to the given point:

`m=(-2--5)/(7-1)=(3)/(6)=(1)/(2)`

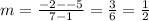
2. The slope of the Tangent at (7,-2) is the Negative (opposite) Reciprocal of the slope of the radius:
`(1)/(2)= > -2`

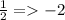
3. Write the equation of the Tangent in Point Slope Form:

`y+2=-2(x-7)`

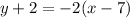
4. Distribute and rewrite in the form ax + by + c = 0

`y+2=-2(x-7)\\y+2=-2x+14\\2x+y-12=0`