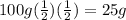Question

There are 100 g of lodine-131. After 16 days, how many grams of lodine-131 is left?

Answer 1

25g

Step-by-step explanation:

According to a quick internet search, the half-life of I-131 is 8 days.

The amount left after 16 days can be calculated with the radioactive exponential decay formula:

`A_(_t_)=A_0e^(^(\ln(.5))/(T)^)^t`

Where:

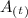`A_(_t_)` = the amount left as a function of time

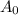`A_0` = the original amount (100g)

T = the half-life of the isotope (8d)

t = time (16d)

So:

`A_(_t_)=A_0e^(^(\ln(0.5))/(T)^)^t\\A_(_t_)=(100g)e^(^(\ln(0.5))/(8d)^)^(^1^6^d^)\\A_(_t_)=(100g)e^-^2^(^\ln(2))`

`A_(_t_)=25g`

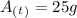
This answer is intuitive because the isotope has been through two half-lives:

`100g((1)/(2))((1)/(2))=25g`