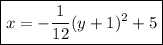Answer:
A. x = 3
B. A = (3, 2)
C. V = (-1, 2)
D. Left
E. See below.
F. p = -4
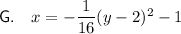
H. See attachment.
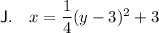
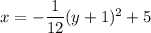
Explanation:
Part A
The given focus of the parabola is F (-5, 2).
The equation for a vertical line is x = a.
Therefore, a vertical line that is 8 units to the right of the focus is:
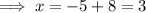
Therefore:
Part B
A line that is perpendicular to the directrix is a horizontal line.
The equation for a horizontal line is y = a.
As the horizontal line passes through the focus:
The point of intersection, A, of the axis of symmetry and the directrix is:
Part C
The vertex of the parabola is the point that is halfway between the focus and the directrix.
Therefore:
Part D
The parabola will open sideways as the axis of symmetry is horizontal.
As a parabola never touches its directrix, this parabola will open to the left.
Part E
The absolute value of p is the distance between the vertex and the focus, and the distance between the vertex and the directrix.
For a sideways parabola, if p > 0 the parabola opens to the right, and if p < 0 the parabola opens to the left.
Part F
Since the focus and directrix are 8 units apart, and the parabola opens to the left:
Part G
Vertex form of a sideways parabola:
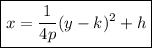
Given:
- Vertex = (-1, 2) ⇒ h = -1, k = 2
- p = -4
Substitute the values into the formula:
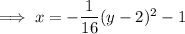
Part H
See attachment.
Part I
Rearrange the equation of the parabola shown in the attachment:
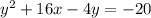
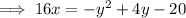
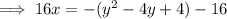
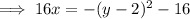
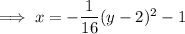
This matches the equation in vertex form in part G.
Part J
Given:
- Focus = (4, 3)
- Directrix: x = 2
Therefore:
- Vertex = ((4+2)/2, 3) = (3, 3)
- Parabola opens to the right, so p > 0.
- p = |4 - 3| = 1
Therefore, the equation of the parabola with the given parameters is:
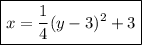
Given:
- Focus = (2, -1)
- Directrix: x = 8
Therefore:
- Vertex = ((8+2)/2, -1) = (5, -1)
- Parabola opens to the left, so p < 0.
- p = -|2 - 5| = -3
Therefore, the equation of the parabola with the given parameters is: