Answer:
f(f(x)) = x, domain is x≠1
Explanation:
You want the domain of f(f(x)), given that f(x) = x/(x-1).
Domain
The domain excludes any value of x where the function is not defined.
The function f(x) = x/(x -1) is undefined at x=1, so that value is excluded from the domain of f(x).
The composite function f(f(x)) can be written as ...
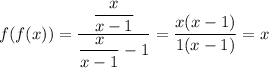
This form shows there are factors of (x-1) in numerator and denominator that cancel. This is what creates the "hole" in the graph of f(f(x)) = x at (1, 1).
The domain of f(f(x)) is x≠1.
<95141404393>