Short Answer:
The given equation has one solution;
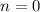 .
.
Further Explanation:
______________________________________________________
"How Can You Determine Whether An Equation Has One Solution, Infinite Solutions, or No Solution?"
- One Solution - Some equations have exactly one solution. In these equations, there is only one value for the variable that makes the equation true. You can tell that an equation has one solution if you solve the equation and get a variable equal to a number.
- Infinite Solutions - Some equations have infinitely many solutions. In these equations, any value for the variable makes the equation true. You can tell that an equation has infinitely many solutions if you try to solve the equation and get a variable or a number equal to itself.
- No Solution - If a linear equation has the same variable term but different constant values on opposite sides of the equation, it has no solutions.
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
This being said, lets now go back to the given scenario and determine the amount of solutions it has, if any.
1. We are given the following to solve:
2. First, subtract 1 from both sides.
3. Simplify.
4. Move 4n to the left side, leaving us with our final solution.
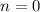 ← Final Solution
← Final Solution
____________________________________________________
Hope this helps!