Question

30 points Please get it Right lol

Graph the piecewise function.

Answer 1

see attached

Explanation:

You want a graph of the piecewise function ...

`f(x)=\begin{cases}x&\text{if $x\le -1$}\\-3x+2&\text{if $-1 < x < 4$}\\4&\text{if $x\ge 4$}\end{cases}`

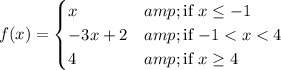
Graph

The graph is attached.

For x ≤ -1, the graph is a line with slope 1. If it were allowed to continue, it would pass through the origin. It terminates in a closed dot at (-1, -1)

For -1 < x < 4, the graph is a line with slope -3 through point (0, 2) on the y-axis. It has open circles at both ends, at points (-1, 5) and (4, -10).

For x ≥ 4, the line is horizontal at y=4. It has a closed dot at (4, 4).

__

Additional comment

The dot at the end of an interval is closed if the "or equal to" case is included (≤ or ≥). If it is not (< or >), then the dot is an open circle.

The slope is the ratio of "rise" to "run". It is the number of grid squares the line moves up (+) or down (-) for each grid square to the right.