Question

Determine the degree measure of one angle of a 36-sided regular polygon. 170° 180° 6,120° 6,480°

Answer 1

If I determine the degree measurement of an angle of a 36 sided regular polygon, it will be 180 degrees, Because one angle of the 36 sided polygon is 180 degrees and you measure it, then this is your top answer.

Hope it helps!

-encey6915

Answer 2

A) 170°

Explanation:

For a regular polygon with "n" sides, the interior angle can be calculated using the formula:

`\text{Interior angle of a regular polygon} = (180^(\circ) \cdot (n - 2))/(n)`

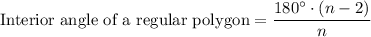
Therefore, to determine the degree measure of one angle of a 36-sided regular polygon, substitute n = 36 into the formula:

`\begin{aligned}\text{Interior Angle} &= (180^(\circ) \cdot (36 - 2))/(36)\\\\&= (180^(\circ) \cdot 34)/(36)\\\\&= (6120^(\circ))/(36)\\\\&=170^(\circ)\end{aligned}`

Therefore, the degree measure of one angle of a 36-sided regular polygon is:

`\Large\boxed{\boxed{170^(\circ)}}`