Answer:
4860 bacteria
Explanation:
The given scenario can be modelled using an exponential function with base e.

Define the variables:
- Let y be number of bacteria.
- Let x be the time (in hours)
Given the initial number of bacteria is 20, then A = 20.
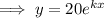
If the bacteria triples its number in 16 hours, then when x = 16:
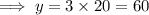
Substitute x = 16 and y = 60 into the equation and solve for k:

Therefore, the equation that models the given scenario is:
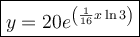
To find how many bacteria there are after 80 hours, substitute x = 80 into the equation and solve for y:
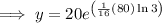
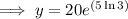
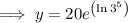
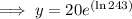
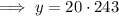
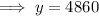
Therefore, there are 4860 bacteria after 80 hours.
-----------------------------------------------------------------------------------------------
Please note that I have solved this question so that you can calculate the number of bacteria for any number of hours, part hours, etc.
However, there is a much simpler way of solving this particular question.
If the number of bacteria triples every 16 hours, then it will triple 5 times within 80 hours since 80 ÷ 16 = 5.
Therefore:
- Hour 0: 20
- Hour 16: 20 × 3 = 60
- Hour 32: 60 × 3 = 180
- Hour 48: 180 × 3 = 540
- Hour 64: 540 × 3 = 1620
- Hour 80: 1620 × 3 = 4860
As you can see, the result is the same as the previous method.