Answer:
(a.) 27^4/3 = 81, (b.) 36^3/2 = 216, (c.) (1/8)^2/3 = 1/4, (d.) 128^5/7 = 32
Explanation:
All these expressions can be converted in square roots.
In order to do this, we can picture the fractional exponents as exponent / index
(a.) So for this first problem, we would have the cube root of
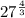 or
or
![\sqrt[3]{(27)^(4) }](https://img.qammunity.org/2023/formulas/mathematics/high-school/kh6o7ev9nl9p9368917zisfrki8v3h6sw8.png) .
.
We must do the equation inside the radical first (i.e.,
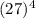 ) to get
) to get
![\sqrt[3]{531,441}](https://img.qammunity.org/2023/formulas/mathematics/high-school/1x2g8mbeci6gplfi2tvbxgyllqxnp0fbix.png) = 81
= 81
We can follow these same steps for the remaining equations:
(b.)
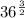 =
=
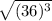 =
=
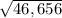 = 216
= 216
(c.)
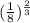 =
=
![\sqrt[3]{((1)/(8))^(2) }](https://img.qammunity.org/2023/formulas/mathematics/high-school/shvg2u3z2z5tvau81y4sn74ied10513blk.png) =
=
![\sqrt[3]{((1^2)/(8^2)) }](https://img.qammunity.org/2023/formulas/mathematics/high-school/ok3z9zzxaug6skbw4hn23idqxq4zqg8rm6.png) =
=
![\sqrt[3]{((1)/(64)) }](https://img.qammunity.org/2023/formulas/mathematics/high-school/btn697ye4aqe8jty7xjzzkpr3mprwsj6aj.png) =
=
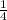
(d.)
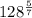 =
=
![\sqrt[7]{(128)^(5) }](https://img.qammunity.org/2023/formulas/mathematics/high-school/r63fsl8mz1r8twxqjfjxy2zb6t27pysc0o.png) = 32
= 32