Answer:
about 2.758 cm/s
Explanation:
You want the rate of change of a cylinder's radius, when its height is 33 cm increasing at 2 cm/s, and its volume is 403 cm³ increasing at 1152 cm³/s.
Rate of change
The volume of a cylinder is given by the equation ...
V = πr²h
Solving for the radius gives ...
r = √(V/(πh))
Differentiating, we have ...
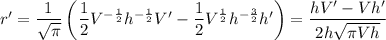
Filling in the values V = 403, V' = 1152, h = 33, h' = 2, we have ...
r' = (33·1152 -403·2)/(2·33·√(π·403·33)) = 37210/(66√(13299π))
r' ≈ 2.758 . . . . . cm/s
The rate of change of the radius is about 2.758 cm/s.