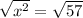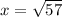Answer:
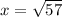
Explanation:
The Pythagorean Theorem states that:
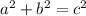
where
 and
and
 are legs of a right triangle (they meet at the right angle), and
are legs of a right triangle (they meet at the right angle), and
 is the triangle's hypotenuse.
is the triangle's hypotenuse.
We can apply this theorem to the given triangle:
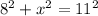 ,
,
and all we have to do is solve for x.
First, simplify all the square roots.
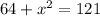
Then, subtract 64 from both sides.
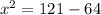

Finally, take the square root of both sides.