Question

If a person travels at a speed of 33 m/s and travels 132 meters, how long does the trip take?

Answer 1

Answer: 4 seconds.

Step-by-step explanation: Simply divide 132 meters by 33 m/s. This gives you four. (as in the trip took four seconds.)

Answer 2

It is a uniform rectilinear movement which is one in which an object moves in a straight line, in one only direction, with a constant speed.

When we spoke of constant speed we mean that the movement retains the same speed, that is; that the object does not move faster, or slower and always at the same speed.

If a person travels at a speed of 33 m/s and travels 132 meters, how long does the trip take?

We obtain the data according to the exercise.

Data:

V = 33 m/s

D = 132 m

t = ?

We have that the uniform motion formula is:

`\large\displaystyle\text{$\begin{gathered}\sf V=(d)/(t), \to where \end{gathered}$}`

• 
  `\large\displaystyle\text{$\begin{gathered}\sf V=Speed \end{gathered}$}`

• 
  `\large\displaystyle\text{$\begin{gathered}\sf D=distance \end{gathered}$}`

• 
  `\large\displaystyle\text{$\begin{gathered}\sf T=Time \end{gathered}$}`

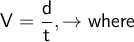
We solve for time, since that is what we are asked to calculate. And substitute data in the formula.

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{t=(d)/(V) } \end{gathered}$}}`

`\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{t=\frac{132 \\ot{m}}{33 \ \frac{\\ot{m}}{s} } } \end{gathered}$}}`

`\boxed{\boxed{\large\displaystyle\text{$\begin{gathered}\sf \bf{t=4 \ s} \end{gathered}$}}}`

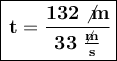
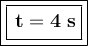
I brought on the trip, a time of 4 seconds.