Answer:
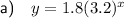
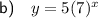
Explanation:

Part (a)
Given ordered pairs:
- (0, 1.8)
- (1, 5.76)
- (2, 18.432)
The y-intercept is the y-value when x = 0.
Therefore, as the y-intercept is 1.8, a = 1.8.
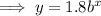
Substitute point (1, 5.76) into the equation and solve for b:
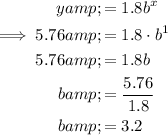
Therefore, the exponential equation is:
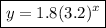
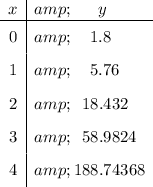
To complete the given table, simply substitute the values of x into the found equation:
Part (b)
Given ordered pairs:
The y-intercept is the y-value when x = 0.
Therefore, as the y-intercept is 5, a = 5.
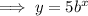
Substitute point (2, 245) into the equation and solve for b:
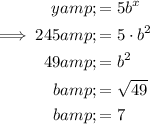
Therefore, the exponential equation is:
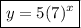
To complete the given table, simply substitute the values of x into the found equation:
