Answer:
2x + y = 25
Explanation:
Given equations:
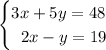
Rearrange the second equation to isolate y:
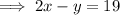
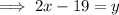
Substitute the found expression for y into the first equation and solve for x:
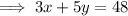
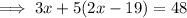
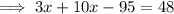
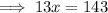
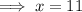
Substitute the found value of x into the equation for y and solve for y:
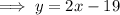
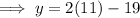
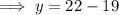
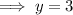
Therefore, the solution of the given system of equations is:
To find the value of 2x + y, substitute the found values of x and y into the expression and solve:
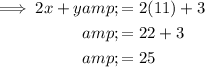
Therefore: