Answer:
x = 25.5°
Explanation:
First find the hypotenuse of the right triangle given by the formula
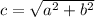
where c is the hypotenuse and a, b the two sides
Let's call the vertical leg as a and the horizontal leg as b
Then we have a = 10, b = 21
So
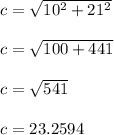
By the law of sines, the ratios of the sides of a triangle to the sine of the angles opposite must be the same. The hypotenuse is opposite the 90° angle. and the side of length 10 is opposite angle x
So
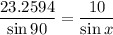
But sin 90 = 1. So the above equation reduces to
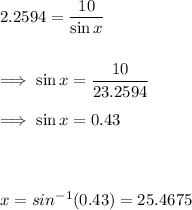
Rounded to 1 decimal place
x = 25.5°