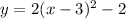Question

Find the quadratic equation whose parabola has vertex (3, –2) and y-intercept (0, 16). Give your answer in vertex form, and show your work.

Please Help!!

Answer 1

y = 2(x-3)^2-2

Explanation:

We can find the quadratic equation by using the vertex form. The vertex form of a quadratic equation is:

`y=a(x-h)^2+k`, where x and y are any point on the parabola, a is the constant (indicating whether the parabola opens up or down), and h and k are the coordinates of the vertex.

Since we already have the y-int (an x and y coordinate lying on the parabola) and the vertex, we can plug in both to find a:

`16=a(0-3)^2-2\\16=a(-3)^2-2\\16=9a-2\\18=9a\\2=a`

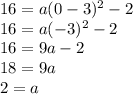
Thus, the equation is:

`y=2(x-3)^2-2`