Question

A town has a population of 17000 and grows at 3% every year. What will be the

population after 10 years, to the nearest whole number?

Answer 1

If the population grows 3% every year, then each year's population is 103% of the previous year's population. This gives us the exponential function:

`f(x) = 17000 (1.03)^x`

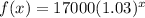
17000 for the current population, 1.03 growth factor for the 103%, raised to the x power because we'll need 103% of 103% of 103% and so on until we multiply by 103% for the correct number of years.

`f(10) = 17000(1.03)^(10) \approx 22846.578448850072648`

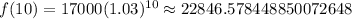
Following standard math rounding this would round to 22,847 people.

If you argue that last 0.57844 of a person really round up, you could argue that this is really 22,846 people.