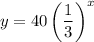Question

NO LINKS!! Based on each graph below, find the equation of the exponential function y= ab^x​

Answer 1

`\textsf{a)} \quad y=3\left((5)/(3)\right)^x`

`\textsf{b)} \quad y=40\left((1)/(3)\right)^x`

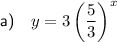
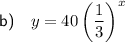
Explanation:

`\boxed{\begin{minipage}{9 cm}\underline{General form of an Exponential Function}\\\\$y=ab^x$\\\\where:\\\phantom{ww}$\bullet$ $a$ is the initial value ($y$-intercept). \\ \phantom{ww}$\bullet$ $b$ is the base (growth/decay factor) in decimal form.\\\end{minipage}}`

Question (a)

From inspection of the diagram, two points on the graph are:

• (0, 3)
• (1, 5)

The y-intercept is the y-value when x = 0.

As a is the y-intercept, and the y-intercept is 3:

`\implies y=3 \cdot b^x`

Substitute point (1, 5) into the equation and solve for b:

`\begin{aligned}(1,5) \implies 5&=3 \cdot b^1\\5&=3b\\b&=(5)/(3)\end{aligned}`

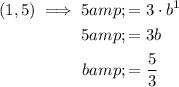
Therefore, the equation of the exponential function is:

`y=3\left((5)/(3)\right)^x`

Question (b)

From inspection of the diagram, two points on the graph are:

• (0, 40)
• (-1, 120)

The y-intercept is the y-value when x = 0.

As a is the y-intercept, and the y-intercept is 40:

`\implies y=40 \cdot b^x`

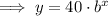
Substitute point (-1, 120) into the equation and solve for b:

`\begin{aligned}(-1,120) \implies 120&=40 \cdot b^(-1)\\(120)/(40)&=(1)/(b)\\b&=(40)/(120)\\ b&=(1)/(3)\end{aligned}`

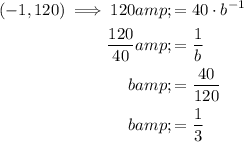
Therefore, the equation of the exponential function is:

`y=40\left((1)/(3)\right)^x`