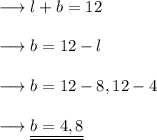Answer:
When l = 4m , breadth is 8m
When l = 8m , breadth is 4m .
Explanation:
Here it is given that the area of a rectangular patch is 32m² . If we assume length to be l and breadth to be b , then ;
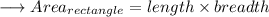
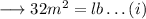
Again , it's given that the perimeter is 24m .We know that perimeter of a rectangle is ,
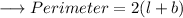
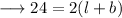
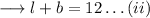
From equation (i) and (ii) , we have ;
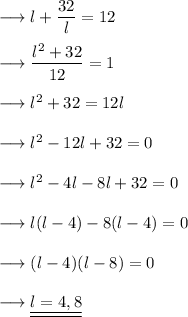
Therefore , we can find breadth as,