Answer:
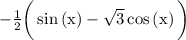
===================================================
Work Shown:
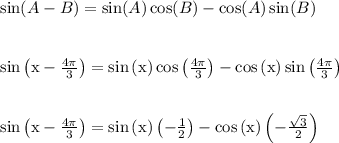
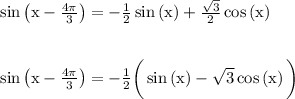
You can a TI83 or TI84 calculator to confirm the answer. Or you can use graphing software tools like Desmos or GeoGebra.
Another approach to verification is using a table of values, but I don't really recommend this option.
The first line I mentioned is one of the many trig identities to either memorize or have on a reference sheet. I prefer the reference sheet option since there are many trig identities to keep track of.
Use the unit circle to determine that
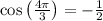 and
and
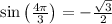 . Look in quadrant III (which is the southwest quadrant).
. Look in quadrant III (which is the southwest quadrant).