Answers:
A triangle is possible.
The triangle is acute and scalene
=============================================================
Step-by-step explanation:
We use the triangle inequality theorem to see if a triangle is possible with these side lengths.
Consider the side lengths a, b, and c. A triangle is possible if and only if the following 3 conditions hold true
Basically pick any two sides. If the sum is larger than the third side, then a triangle is possible.
-----------------
In this case we have: a = 8, b = 14, c = 16. The order of the a,b,c values doesn't really matter.
Then:
- a+b = 8+14 = 22 which is larger than c = 16. So a+b > c is true.
- a+c = 8+16 = 24 is larger than b = 14. So a+c > b is true.
- b+c = 14+16 = 30 is larger than a = 8. So b+c > a is true.
All three inequalities mentioned are true; therefore, a triangle is possible with these side lengths.
-----------------
We'll use those a,b,c values in the converse of the pythagorean theorem to determine what kind of triangle this is. So far we know it's scalene because all three side lengths are different. It would be isosceles if it had exactly two equal sides, and equilateral if all 3 sides were the same length.
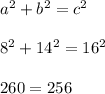
The last equation is false, which tells us this triangle is not a right triangle. It's either acute or obtuse.
Since
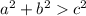 is the case here, we can conclude the triangle is acute
is the case here, we can conclude the triangle is acute
If
 was the case, then the triangle would be obtuse.
was the case, then the triangle would be obtuse.
-----------------
Summary:
- A triangle is possible with side lengths a = 8, b = 14, c = 16.
- This triangle is scalene and acute