Question

Simplify into a single logarithm:

7log4m - 3log45 - 2log4b

Explain your process in one sentence (or more if you need).
Need help please

Answer 1

Answer:
`\log_(4)\left((m^7)/(125b^2)\right)`

================================================

Work Shown:

`7\log_(4)(m)-3\log_(4)(5)-2\log_(4)(b)\\\\\log_(4)(m^7)-\log_(4)(5^3)-\log_(4)(b^2) \ \ \text{... see note1 below}\\\\\log_(4)(m^7)-\log_(4)(125)-\log_(4)(b^2)\\\\\log_(4)(m^7)-\big(\log_(4)(125)+\log_(4)(b^2)\big) \\\\\log_(4)(m^7)-\log_(4)(125b^2)\ \ \text{... see note2}\\\\\log_(4)\left((m^7)/(125b^2)\right) \ \ \text{... see note3}\\\\`

• Note1: Use the log rule B*log(A) = log(A^B)
• Note2: Use the rule log(A)+log(B) = log(A*B)
• Note3: Use the rule log(A)-log(B) = log(A/B)

-------------------

As for the explanation process to your teacher, you can mention each rule verbally or using symbolic notation as I have done above. In my opinion, the steps in the "work shown" section should be sufficient.

Verbally describing the rule in note2 for instance could go something like "the sum of two logs is the same as the log of the product of the arguments". There is probably a more elegant way to state this rule verbally, so feel free to explore various creative options.

Keep in mind that the logs must be the same base for the log rules to apply. Something like
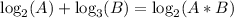`\log_(2)(A)+\log_(3)(B) = \log_(2)(A*B)` is NOT valid.