Question

Please help me I don’t understand

Answer 1

`y = (3)/(2)x + 5`

y = (3/2)x + 5

Explanation:

The format of an equation of a line is
`y = mx + b`. Y and X are the coodinates of a point along the line. b is the y intercept (where it crosses the Y axis). m is the slope. This format is called slope-intercept form.

First, you need to find the slope of the line. You can do this using the slope formula, which is
`m = (y_(2)-y_(1))/(x_(2)-x_(1))`.
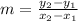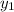`y_(1)` and
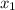`x_(1)` are the x and y values of a point along the line, and
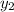`y_(2)` and
`x_(2)` are the x and y values of a different point along the line that has a greater x value. Lastly,
`m` is the slope of the equation, same as slope-intercept form.

To find the slope, you have to plug in your points. (-4, -1) has a smaller X value so we'll replace the
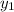`y_(1)` and
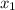`x_(1)` with those coordinates. We'll replace
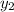`y_(2)` and
`x_(2)` with the other point, (2, 8)'s coordinates.

Now, the equation is
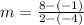`m = (8-(-1))/(2-(-4))`. TO solve, just simplify the right side. 8 minus negative one is 9 (since subtracting negative numbers is the same as adding. 2 minus negative 4 is 6. Now we're left with
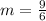`m = (9)/(6)`, and 9 over 6 simplifies to
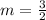`m = (3)/(2)`. So the slope is
`(3)/(2)`, or 1.5. This means the Y value goes up 1.5 for every 1 the x value goes up.

Now, you have to find the Y intercept. To do this, you can make a table and fill in missing values by adding the slope to the Y every time we increase the X:

x | y
-----------
-4 | -1
-3 | 0.5
-2 | 2
-1 | 3.5
0 | 5

Since the X is 0, the line is crossing the Y axis at (0, 5). The y intercept is 5.

Now finally, you just have to plug in the slope and y intercept into slope-intercept form, which is
`y = mx + b`, as mentioned above. B is the y intercept, so we replace that with five, making
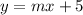`y = mx + 5`. M is the slope, so you replace that with
`(3)/(2)`. This makes the equation
`y = (3)/(2)x + 5`. And that's your answer!

Hopefully this helps, good luck!