Question

Geometry questions....help me someone please

Answer 1

Triangle 1: x = 80 degrees, acute

Triangle 2: x = 10 degrees, right

Explanation:

Triangle 1:

By the Sum of Interior Angles Theorem, all the angles inside the triangle adds up to 180 degrees. So, set up this equation:

`60 + 40 +x = 180`

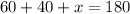
Solve for x:

`100 + x = 180\\x = 80`

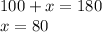
So, x = 80 degrees

Because all the angles are less than 90 degrees, this is an acute triangle.

Triangle 2:

By the Sum of Interior Angles Theorem, all the angles inside the triangle adds up to 180 degrees. So, set up this equation (with the right angle given):

`3x + 60 + 90 = 180`

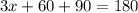
Solve for x:

`3x + 150 = 180\\3x = 30\\x = 10`

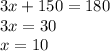
So, x = 10 degrees

Because there is an angle measuring 90 degrees, this is a right triangle.