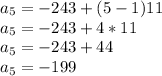Answer:
a5 = -199
Explanation:
The formula to find the nth term in an arithmetic sequence is:
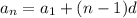 , where a1 is the first term, n is the term position (e.g. 5th, 13th), and d is the common difference.
, where a1 is the first term, n is the term position (e.g. 5th, 13th), and d is the common difference.
To find a5, we at least need to find a1. We can plug in a13 (-111) for an and 13 for n:
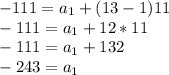
Since we now know a1, we can find find a5 (remembering to plug in 5 for n):