Question

What is the slope of a line parallel to the line whose equation is 3x+4y=36. Fully simplify your answer.

Answer 1

`-(3)/(4)`

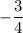
Explanation:

Convert the equation to slope intercept form:

`y=mx+b`,

as in that form,
`m` can be identified as the slope of the line.

First, move the x's to the right side.

`3x+4y=36\\\underline{-3x \ \ \ \ } \ \ \ \ \, \underline{-3x}`

`4y = 36 - 3x`

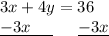
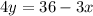
Then, divide both sides by 4 to isolate one multiple of y.

`4y = 36 - 3x\\\overline{\ 4 \ } \ \ \ \, \overline{\, \ \ \: \ 4 \ \ \ \, \ }`

`y = 9 - (3)/(4)x`

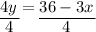
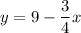
And reorder the right side to fit slope-intercept form.

`y = - (3)/(4)x + 9`

Finally, identify the slope as

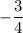`-(3)/(4)`.