Question

Write an equation for each line. Then graph the line. Through (-1,3) and parallel to y = 2x+1

Answer 1

keeping in mind that parallel lines have exactly the same slope, let's check for the slope of the equation above

`y=\stackrel{\stackrel{m}{\downarrow }}{2}x+1\qquad \impliedby \begin{array} \cline{1-1} slope-intercept~form\\ \cline{1-1} \\ y=\underset{y-intercept}{\stackrel{slope\qquad }{\stackrel{\downarrow }{m}x+\underset{\uparrow }{b}}} \\\\ \cline{1-1} \end{array}`

so we're really looking for the equation of a line whose slope is 2 and it passes through (-1 , 3)

`(\stackrel{x_1}{-1}~,~\stackrel{y_1}{3})\hspace{10em} \stackrel{slope}{m} ~=~ 2 \\\\\\ \begin{array} \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-\stackrel{y_1}{3}=\stackrel{m}{ 2}(x-\stackrel{x_1}{(-1)}) \implies y -3= 2 (x +1) \\\\\\ y-3=2x+2\implies {\Large \begin{array}{llll} y=2x+5 \end{array}}`

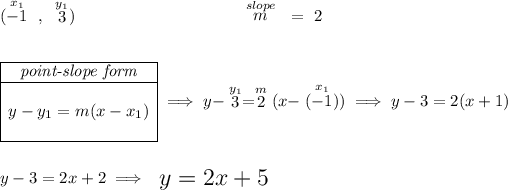
now, to graph a line, we only need two points and connect them through, well, hell we already have (-1 , 3), let's get another hmmm

say if x = 2

y = 2(2) + 5 => y = 9

that gives us the 2nd point of (2 , 9)

Check the picture below.