Answer:
a) f(x) = 12x +11
b) f(x) = 12(x +11)
c) f(x) = x/2 -6
d) f(x) = (x -6)/2
Explanation:
The "and then ..." operation applies to the entire result of the first operation.
a)
"multiplies input by 12" = 12x
"and then adds 11" = 12x +11
f(x) = 12x +11
__
b)
"adds 11 to the input" = x +11
"and then multiplies by 12" = (x +11)×12 = 12(x +11)
f(x) = 12(x +11)
__
c)
f(x) = x/2 -6
__
d)
f(x) = (x -6)/2
_____
Additional comment
When you write division expressions in plain text using a slash (/) or "divided by" symbol (÷), you need to be careful to identify what the numerator and denominator are. If either one is other than a single token (variable or constant), then parentheses must be used to indicate what is part of the group.
In typeset text, the answer to (d) looks like ...
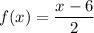
If you write this in plain text as ...
f(x) = x -6/2
the Order of Operations requires that you do the division first, giving 6/2 = 3, then the subtraction: x -3. Of course, this result is something entirely different from the f(x) described in part (d). In short, the fraction bar in the typeset expression serves as a grouping symbol, so (x -6) is treated as a single unit. In plain text, the only grouping symbol available is parentheses, so the expression must be written as ...
f(x) = (x -6)/2
__
The same sort of logic applies to other typeset symbols that do grouping. A radical is another one of these:
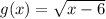
is not the same as g(x) = √x -6. However, it is the same as g(x) = √(x -6).