Question

A police car is driving north with a siren making a frequency of 1038 hz. Moops is driving north behind the police car at 12 m/s and hard a frequency of 959hz. How fast is the police car going?

Answer 1

The police car is moving at 41.24 m/s.

Step-by-step explanation:

To find the speed of the police car we need to use the Doppler equation:

`f = f_(0)((v + v_(r))/(v + v_(s)))`

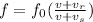
Where:

v: is the speed of the sound = 343 m/s

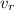`v_(r)`: is the speed of the receiver = 12 m/s

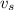`v_(s)`: is the speed of the source =?

f: is the observed frequency = 959 Hz

f₀: is the emitted frequency = 1038 Hz

Both terms are positive in the fraction because the velocity of the sound is in the opposite direction to both velocities of the police car and the other car.

By solving the above equation for
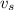`v_(s)` we have:

`v_(s) = (f_(0)(v + v_(r)))/(f) - v = (1038(343 + 12))/(959) - 343 = 41.24 m/s`

Therefore, the police car is moving at 41.24 m/s.

I hope it helps you!