Final answer:
The function f(x) = -
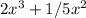 does not have a horizontal asymptote because the highest degree of x in the polynomial is greater than zero, indicating that the function's value approaches infinity as x approaches infinity.
does not have a horizontal asymptote because the highest degree of x in the polynomial is greater than zero, indicating that the function's value approaches infinity as x approaches infinity.
Step-by-step explanation:
To find the equation of the horizontal asymptote of a function, we look at the behavior of the function as x approaches infinity. For the function f(x) =
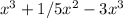 , we must first correct it by consolidating like terms. This gives us f(x) = -
, we must first correct it by consolidating like terms. This gives us f(x) = -
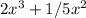 . In polynomial functions, horizontal asymptotes are determined by the degree of the highest power term in the numerator and the denominator (if any).
. In polynomial functions, horizontal asymptotes are determined by the degree of the highest power term in the numerator and the denominator (if any).
Since the highest power of x in f(x) is cubic and there is no denominator (or we can consider the denominator as 1 which is a constant), as x approaches infinity, the function will also approach infinity. Therefore, there is no horizontal asymptote for this kind of polynomial function. A horizontal asymptote would only be present if the highest power of x in the numerator was less than or equal to the highest power of x in the denominator for rational functions.