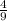Question

HELP!!! A set of 3 cards, spelling the word ADD, are placed face down on the table. Determine P(D, D) if two cards are randomly selected with replacement.

1/3
2/3
2/6
4/9

Answer 1

Answer: P(D, D) =
`(4)/(9)`

Explanation:

An important thing to note for this question is that the cards are randomly selected with replacement. This means that the chances to pick a specific card do not change for each draw. This is called an independent event.

The next thing to note is the cards. We have A, D, and D. This means that out of the set, two of the three cards are D. To find the probability, we will divide the number of cards we're trying to draw by the total number of cards.

P(D) =
`(2)/(3)`

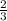
Next, we need to find the probability of drawing two D's, one after the other. To do this, we will multiply the probability of drawing one D together twice. We can do this since it's an independent event.

P(D, D) =
`(2)/(3)` *
`(2)/(3)`

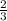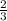
P(D, D) =
`(4)/(9)`