Question

The quadratic equation x + k + 9/x = 0 has equal roots. Find the two possible values of k.

Answer 1

k = 6 or k = -6

Explanation:

The standard form of the quadratic equation is

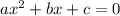`ax^(2)+bx+c=0` ....[1]

The roots of this equation can be determined using the quadratic formula:

`x = ( -b \pm √(b^2 - 4ac))/( 2a )`

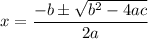
When
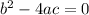`b^2-4ac = 0` there is one real root

When
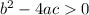`b^2-4ac > 0` there are two real roots

When
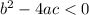`b^2-4ac < 0` there are two imaginary roots

First let's convert the equation

`x + k + (9)/(x) = 0`

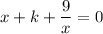
into its standard form by multiplying both sides by x
We get

`x^2 + kx + 9 = 0` [2]

By comparing this standardized form to the general standard form we can see that the coefficient of x², namely a is 1, the coefficient of x, namely b is k and c is 9

So we have
a = 1
b = k
c= 9

Since we are given that there is only one root and therefore b²-4ac = 0 lets plug in these values of a, b and c
We get k² - 4·1·9 = 0
==> k² - 36 = 0
==> k² = 36
==> k = ±√36
===> k = ±6

So the two possible values of k are k = 6 and k = -6
So the equations become

x² + 6x + 9 = 0 whose roots are x = -3 and x = -3
and
x² -6x + 9 = 0 whose roots are x = 3, x = 3

In both cases the roots are the same

Hope that helps