Question

What is the complete factorization of the polynomial function over the set of complex numbers?

f(x) = x^3-4x^2 + 4x - 16

Answer 1

(x - 4)(x + 2i)(x - 2i)

Explanation:

f(x) = x³ - 4x² + 4x - 16 ( factor the first/second and third/fourth terms )

= x²(x - 4) + 4(x - 4) ← factor out (x - 4) from each term

= (x - 4)(x² + 4)

set x² + 4 = 0 ( subtract 4 from both sides )

x² = - 4 ( take square root of both sides )

x = ±
`√(-4)` = ±
`√(4(-1))` = ± (
`√(4)` ×
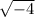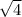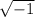`√(-1)` ) = ± 2i , so

x² + 4 = (x + 2i)(x - 2i)

Then

f(x) = x³ - 4x² + 4x - 16 = (x - 4)(x + 2i)(x - 2i)