Answer:
8. 14√2
9. 3∛5
10. -15∛5
Explanation:
You want simplified forms of the radicals √392, ∛135 and -3∛625.
Factoring
For simplifying radicals, a useful first step is factoring the radicand to primes. Then the index can be applied to the exponents, and any integer results will be the factors that go outside the radical.
8.
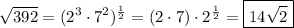
9.
![\sqrt[3]{135}=(3^3\cdot5)^{(1)/(3)}=(3)(5^{(1)/(3)})=\boxed{3\sqrt[3]{5}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/82owxuqpuyxy2aq3tnc14yhcv3882d2u6f.png)
10.
![-3\sqrt[3]{625}=(-3)(5^4)^{(1)/(3)}=(-3\cdot5)(5^{(1)/(3)})=\boxed{-15\sqrt[3]{5}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/nv6bx36cauwnuh0m3huzl64ep3zk7rxba3.png)