Question

A planet has twice the mass of Earth. How much larger would the radius of the planet have to be for the gravitational field strength, gat the planet's surface to be the same as on Earth's surface?

Answer 1

Step-by-step explanation:

Ginen:

g - free fall acceleration on Earth

M - mass of the Earth

g₁ = g - acceleration of free fall on the planet

M₁ = 2·M - Mass of the planet

______________

R₁ / R - ?

`g =(G\cdot M)/(R^2) \\`

`g_1 =(G\cdot M_1)/(R_1^2) \\\\`

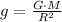
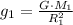
Equate:

`(G\cdot M)/(R^2) = \frac{G\cdot M_1} {R_1^2}\\\\(G\cdot M)/(R^2) = \frac{G\cdot 2M} {R_1^2}\\\\(1)/(R^2) = \frac{2} {R_1^2}\\\\\\`

`R_1=√(2)\cdot R\\\\(R_1)/(R) = √(2) \\`

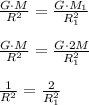
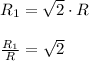
The radius of the planet is √2 times greater than that of the Earth

Планета имеет массу в два раза больше Земли. Насколько больше должен быть радиус планеты для напряженности гравитационного поля, если поверхность планеты будет такой же, как на поверхности Земли?