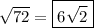Question

Algebra 1, unit 1 Lesson 8 homework. I need help understanding.

Answer 1

3. ∛200 = ∛20∛10 = ∛8∛25

4. √72 = √3√24 = √36√2

5. ∛200 = 2∛25

6. √72 = 6√2

Explanation:

You want the radicals ∛200 and √72 each written in two different forms, one of which simplifies to the product of an integer and a radical. Then you want to see that simplified product.

Exponent rules

One of the rules of exponents is that a power of a product is the product of the powers:

(ab)^c = (a^c)(b^c)

A radical is equivalent to a fractional exponent.

`\sqrt[n]{a}=a^{(1)/(n)}\\\\√(a)=a^{(1)/(2)}`

Combining these, we get ...

`\sqrt[n]{ab}=\sqrt[n]{a}\cdot\sqrt[n]{b}`

3.

`\sqrt[3]{200}=\sqrt[3]{20}\sqrt[3]{10}\\\\\sqrt[3]{200}=\sqrt[3]{8}\sqrt[3]{25}`

4.

`√(72)=√(3)√(24)\\\\√(72)=√(36)√(2)`

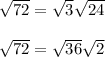
5.

`\sqrt[3]{200}=\boxed{2\sqrt[3]{25}}`

6.

`√(72)=\boxed{6√(2)}`