Question

Section 8.1 Introduction to the Laplace Transforms

Problem 8.

Use the known Laplace transform L(1)=1/s and the result of Exercise 6 to show that

`L( {t}^(n) ) = \frac{n!}{ {s}^(n + 1) } , \: n = integer.`
​

Answer 1

Presumably you've proven exercise 6, that the Laplace transform of
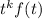`t^k f(t)` is
`(-1)^k F^((k))(s)`.

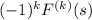Let F(s) = 1/s, whose inverse Laplace transform is f(t) = 1. Differentiate F with respect to s :

`F'(s) = -\frac1{s^2}`

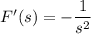
By the claim from ex.6, this is the Laplace transform of t • f(t) = t.

Differentiate F again with respect to s :

`F''(s) = \frac2{s^3}`

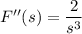
and this is the Laplace transform of t² • f(t) = t². And so on.

We can prove the general claim by induction. Assume it's true for n = k, that
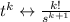`t^k \leftrightarrow (k!)/(s^(k+1))`. Then using the result of ex.6, we have

`F(s) = (k!)/(s^(k+1)) \implies F'(s) = -((k+1)!)/(s^(k+2)) \leftrightarrow t^(k+1)`

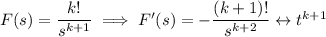
QED