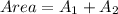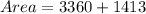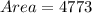Answer:
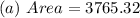
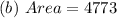
Explanation:
Given
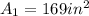 --- area of each square
--- area of each square
See attachment for window
Solving (a): Area of the window
First, we calculate the dimension of each square
Let the length be L;
So:
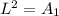
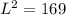
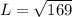
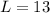
The length of two squares make up the radius of the semicircle.
So:
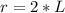
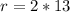
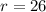
The window is made up of a larger square and a semi-circle
Next, calculate the area of the larger square.
16 small squares made up the larger square.
So, the area is:
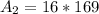
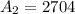
The area of the semicircle is:

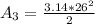
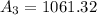
So, the area of the window is:
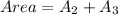
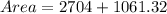

Solving (b): Area of the shade
The shade extends 4 inches beyond the window.
This means that;
The bottom length is now; Initial length + 8
And the height is: Initial height + 4
In (a), the length of each square is calculated as: 13in
4 squares make up the length and the height.
So, the new dimension is:
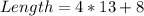
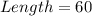
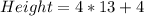
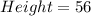
The area is:
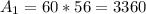
The radius of the semicircle becomes initial radius + 4
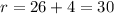
The area is:
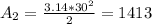
The area of the shade is: