Answer:
(2n -5)(3n -2)
Explanation:
You want to factor 6n² -18n +10.
Sum and product
You want to start by finding factors of the product (6)(10), the first and last coefficients, that have a sum equal to -18, the linear term coefficient.
This sum is negative, but the product is positive, so both factors will be negative. Listing the smallest magnitude first, we have ...
60 = (-1)(-60) = (-2)(-30) = (-3)(-20) = (-4)(-15) = (-5)(-12) = (-6)(-10)
The sums of these pairs are -61, -32, -23, -19, -17, -16. This identifies the pair of interest as (-4)(-15).
Final steps
From here, there are a couple of ways you can proceed. One is to write the linear term as a sum using these values:
6n² -4n -15n +10
Now, you can factor by grouping:
= (6n² -4n) -(15n -10)
= 2n(3n -2) -5(3n -2)
= (2n -5)(3n -2) . . . . . . . . the factorization you want
Another way you can do this is to write binomial factors using the leading coefficient for each one. The product of these must be divided by the leading coefficient for it to remain equal to the original trinomial.
= (6n -4)(6n -15)/6
The denominator of 6 is used to reduce each of the binomial factors.
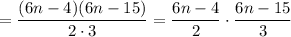
= (3n -2)(2n -5) . . . . . . . the factorization you want