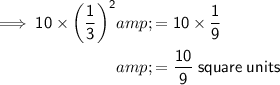Question

Can someone Help pleasee!!!!

Answer 1

`\sf a) \quad k=4 \longrightarrow 160\;square\;units`

`\sf b) \quad k=1.5 \longrightarrow 22.5\;square\;units`

`\sf c) \quad k=1 \longrightarrow 10\;square\;units`

`\sf d) \quad k=(1)/(3) \longrightarrow (10)/(9)\;square\;units`

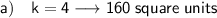
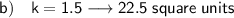
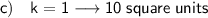
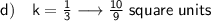
Explanation:

As area is measured in units squared, when dilating an area, multiply it by the square of the scale factor.

Given area of the polygon:

• 10 square units

(a) For a scale factor of 4, the area of the dilated polygon is:

`\begin{aligned}\implies \sf 10 * 4^2&=\sf 10 * 16\\ &= \sf 160\;square\;units \end{aligned}`

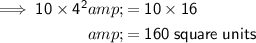
(b) For a scale factor of 1.5, the area of the dilated polygon is:

`\begin{aligned}\implies \sf 10 * 1.5^2&=\sf 10 * 2.25\\ &= \sf 22.5\;square\;units \end{aligned}`

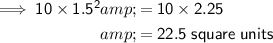
(c) For a scale factor of 1, the area of the dilated polygon is:

`\begin{aligned}\implies \sf 10 * 1^2&=\sf 10 * 1\\ &= \sf 10\;square\;units \end{aligned}`

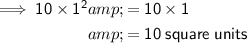
(d) For a scale factor of ¹/₃, the area of the dilated polygon is:

`\begin{aligned}\implies \sf 10 * \left((1)/(3)\right)^2&=\sf 10 * (1)/(9)\\ &= \sf (10)/(9)\;square\;units \end{aligned}`